移動体(航空機や自動車など),特に無人機の慣性航法に興味を持つ学生や技術者が,慣性航法の理論と応用を理解することができるように,以下の内容について,わかりやすく紹介していく予定です.
- 序論
- 行列とベクトル
- 座標系と座標変換
- 地球モデル
- 姿勢
- 不規則過程とアラン分散
- カルマンフィルタ
- 慣性航法の運動方程式
- 慣性航法装置のカルマンフィルタ
- 付録
第1章「序論」では移動体(航空機や自動車など)の座標系,慣性計測装置と慣性センサ,慣性航法と複合航法についてその概要を説明します.4頁,図表4.

pdfを読む → Chapter1_Introduction_03
第2章「行列とベクトル」では慣性航法の理論を理解するのに必要な範囲で,行列とベクトルの公式をその計算例とともに説明します.19頁
pdfを読む → Chapter2_Matrix & Vector_02
第3章「座標系と座標変換」では慣性航法に必要な座標系について説明します.次いで,それらの座標系間の座標変換を表す方法である方向余弦行列とオイラー角について図解を加えてくわしく説明します.17頁,図表16
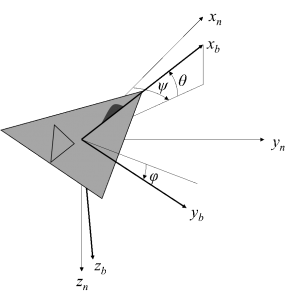
pdfを読む → Chapter3_Frames & Transformations_04
第4章「地球モデル」の前半では地球の形(回転楕円体)と自転角速度についてくわしく説明します.19頁,図表10
pdfを読む → Chapter4-1_Earth Models_06
第4章「地球モデル」の後半では地球の重力(Somiglianaの式など)についてくわしく説明します.22頁,図表6
pdfを読む → Chapter4-2_Earth Models_06
第5章「姿勢」の前半では移動体の姿勢を表現するのに強力なツールとなるクォータニオン(quaternion)を導入し,方向余弦行列やオイラー角との相互関係をくわしく説明します.21頁,図表9
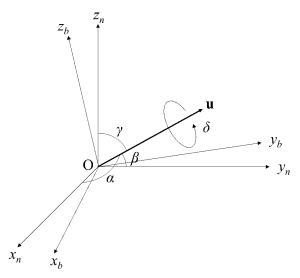
pdfを読む → Chapter5-1_Attitude_05
第5章「姿勢」の後半では移動体の姿勢(オイラー角,方向余弦行列,クォータニオン)の時間微分と角速度(ジャイロの出力)との関係,姿勢誤差,姿勢計測についてくわしく説明します.姿勢誤差は慣性航法の微分方程式に必要となります.21頁,図表2
pdfを読む → Chapter5-2_Attitude_06
第6章「不規則過程とアラン分散」の前半ではセンサノイズの数学モデルである不規則過程(random process)の自己相関係数とパワースペクトル密度についてくわしく説明します.後半のアラン分散の準備となります.14頁,図表8
pdfを読む → Chapter6-1_random process and Allan variance_01
第6章「不規則過程とアラン分散」の後半ではセンサノイズのモデル化に非常に役立つアラン分散(Allan variance)についてくわしく説明します.20頁,図表17
pdfを読む → Chapter6-2_random process and Allan variance_01
第7章「カルマンフィルタ」では慣性航法アルゴリズムに不可欠なカルマンフィルタ(Kalman filter)についてくわしく説明します.18頁,図表6
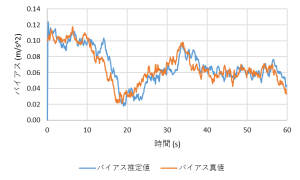
pdfを読む → Chapter7_Kalman filter_03
第8章「慣性航法の運動方程式」では,移動体の運動方程式(位置方程式,速度方程式,姿勢方程式の3個の方程式)と,それらをカルマンフィルタに利用するための誤差方程式をくわしく説明します.26頁,図表6
pdfを読む → Chapter8_navigation equations_06
第9章「慣性航法装置のカルマンフィルタ」では,拡張カルマンフィルタ(第7章)のアルゴリズムに,慣性航法の運動方程式(第8章)を適用して,慣性航法装置のカルマンフィルタを導き,無人機の飛行シミュレーションを行います.チュートリアル全体を通じての例題となっています.19頁,図表9
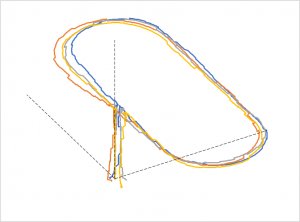
pdfを読む → Chapter9_Kalman filter for INS_03
「付録」 本書の参考文献,記号表,索引を紹介します.9頁
pdfを読む → Appendix_03